NHK Eテレ「考えるカラス」第6回の「考える練習『糸巻き』」の問題はこちら
今日は、糸巻(ま)きを使った問題です。机(つくえ)の上に糸巻きをおきます。少し糸が出ています。ここからが問題。この糸を、水平に引っぱります。糸巻きはどう動くのでしょうか。1.うしろ向きに回転して手からはなれる。2.前向きに回転して引っぱった手に近づく。3.その場で空回りして動かない。*2
解答は…
考える練習「糸巻(ま)き」の答えです。1.手からはなれる。2.手に近づく。3.その場で空回りして動かない。やってみると…、糸巻きは引っぱった手の方向に転がってきます。答えは「2」でした。今度は小さな糸巻きでやってみます。糸を引っぱるとやっぱり手の方向に転がってきました。どうしてこうなるのでしょう。それは、この糸巻きの…。ここから先は、自分で考えよう。これからはみんなが、考えるカラス。
…というわけで、「考えるカラス」には解説が無いけれど、Eテレのサイトには教育用の解説のビデオクリップがあって、全部ネタバレしている。
www2.nhk.or.jp
ひとつだけこの説明に「抜け」があるとすれば、「糸を引くと、必ず糸巻きの軸の円の接線の向きに引く」から、支点と作用点を繋いだ線と糸を引く力の向きの線の関係が説明のとおりになるということ。(…てゆーか、力の分解は中学理科なので、小学生向けの理科でやって、みんなついてこれるのかな?)
以下、自分用の覚書。Google検索の上位に意外とガチの答案がない。
運動方程式
大学で習う剛体の運動方程式*3。「ころがり」の条件で運動方程式を解いてみる。
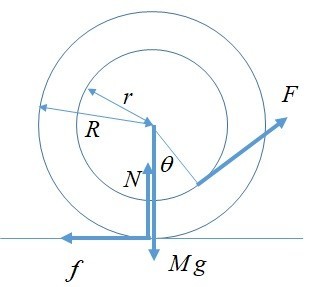
「ころがり」の物体の動き
「ころがる」という状態は、
- 接地点は「瞬間的に速度ゼロ」、それ以外の点は「瞬間的に接地点を中心として回転する向き」に動く(多分、ここが一番想像が難しいところかも)、
- だから、てこを使った説明では接地点が「てこの支点」になる、
- 計算では回転の角速度が
(反時計回りが正)のとき、糸巻の加速度は
(反時計回りなら左へ進む)になる。
宙に浮かない条件
宙に浮かない条件*4は.
回転の角速度と摩擦力
回転、左右の式を,
について解くと
角加速度:, 摩擦力:
「ころがり」である条件
ころがる(すべらないで回る)*5条件は、が最大静止摩擦力
より小:
右へ行く条件
釣り合うのは角加速度(時計回り)より、
だから、糸を引く向きの線(下図の赤線)を伸ばすと、どんぴしゃ接地点を通る。「魔法の手綱」の解説どおりの答えが出ている。

(時計回り)より、
(角度
が浅い方)。この答えを見た上で「考えるカラス」を見直すと、小さい糸巻きを引くときに、蒼井優さんはかなり慎重に水平に糸を引いているのがわかる。
某掲示板のスレ
【悲報】 理系大学生、正答率9%の問題がコチラァ!wywywywywywywywywywywywywywywywywywywywywywywy
とあるまとめサイトでこのスレを見かけたのだが、スレに貼られていた問題の解説(理科教育関連の著書の写真;>>119に貼られている)を見ると、著者の説明が糸を斜めに引いたときに全く応用の利かない推論になっていて、こんなリクツで「応用ができない」とdisられたのでは学生たちはたまったものではないと思う。初等力学の剛体の運動に関する深い(「複雑な」ではなく「核心を突いた」)理解が必要である。これは「考えるカラス」が取り上げるくらいの「意外な答え」の問題である。
*1:画像出典: https://www.nhk.or.jp/das/image/D0005110/D0005110306_00000_C_006.jpg
*2:出典: #6 | 考えるカラス~科学の考え方~ | NHK for School
*3:かつて高校の「物理Ⅱ」に入っていた時期もあった。学習指導要領データベースインデックス 第4節 理科
*4:糸を斜め上に強く引くと、糸巻は宙に浮く…くらいは想像がつく。
*5:力学の教科書では「ころがり」とは接地点で「糸巻の接地点」の対地速度がゼロということ。よって静止摩擦力で計算しないといけない。
