卵と壁？あるいは京大の音波の問題を解いてみた

[2019.1.19追記]このエントリは、点音源近似が音源近傍で破綻することに目をつぶり、えいやっと変位は固定端、圧力は自由端反射モデル（閉管の共鳴の境界条件）で反射を求め、速度ポテンシャル（あるいは圧力）の分布を用いた〈位相差当てゲーム〉を音源に適用すれば、高校の物理で学習する処理の範囲内で解けるという方針で解いている■　この京大の出題には2個の問題点がある。一つ目は高校物理のおやくそくである点音源近似（同心円状の波面を想定して、[振幅の減衰を気にせずに]波の位相だけを当てること）が現実には破綻している点（同心円の中心点、すなわち音の発生源）での状態を問うていること。二つ目は高校物理で学習する範囲内では音波の反射について「閉管での反射」「開管での反射（←このエントリを書いたときはすっかり忘れてた）」しかモデルが無いのに、音波の透過と反射の双方を問うているので、壁での境界条件として高校物理の範囲内のどちらのモデルを想定して計算すればいいのか（実際問題としては壁での透過と反射が共存するとそのどちらでもないのだが）、問題文からは不明瞭であることである■　とは言うものの、高校物理は（本来は現象の核心を理解するための）「近似」「モデル化」のオンパレードなので、どこまでが出題として許容されるのかの判断が難しいと思う■

今度は京大か？新聞の論調はまるで「卵と壁」（村上春樹）みたいだ。でも本当にそうか？

計算をしてみた結論として「言いがかりに近いのではないか？」という感想を持った。阪大の~~『解答』~~問題設定は露骨にヘマだったが、京大の問題は受験の問題として良問ではないかと思う。Twitterなどでの議論で最悪の点は、議論で使う語を「高校物理」の範囲に無理やり押し込めようとして、式で書いたら明快な部分を不明瞭にしてしまっていることだ。まずはきっちりと解いて、それから「高校の知識に落とし込めるか？」を考える方が良い（この点で件のSEG/河合塾の先生の議論はイマイチで大学の大先生たちを説得できないと思う）。

まずは大学の学部程度で学習する水準の知識で力任せに壁での入射波、反射波を解く

流体の基礎方程式である連続の式とオイラー方程式を念頭に置きながら解く。まず速度は回転成分を持たないから速度ポテンシャル $\phi(x,y,t)$ を用いて $\boldsymbol{u}=\nabla\phi$ と書くことができる。このときオイラー方程式は $\frac{\partial}{\partial t}\nabla\phi=-\frac{1}{\rho_0}\nabla p$ となるので、速度ポテンシャル（の $t$ 偏導関数）と圧力が「逆向きのでこぼこを持つ関数」、つまり等高線を描くと同じ形になる関数とわかる。このことは後で波の干渉を議論するときに使う。

ここで高校物理で「ドップラー効果」をお勉強するときに、「音源を出てから聞き取るまでに波が走る行路の長さ」を測る計算のお約束として、点音源から同心円状に広がる波面を考える。 $(L,0)$ の位置にあるずーーーっとなり続けている音源(source)から軸対称に放射される音波の速度ポテンシャルは

$\phi_s(x,y,t)=F(\sqrt{(x-L)^2+y^2})\sin[2\pi f(t-\frac{\sqrt{(x-L)^2+y^2}}{c})]$

で与えらえる*1。ここで振幅 $F$ は音源からの距離の関数であり、音源から遠いほど波面が広がっていくから、振幅 $F$ は小さくなってゆくはずである（…が、ここでは $F$ の関数形を求めない）。

さて、壁での反射波(refrection)の速度ポテンシャルは（波面の形を描くと分かるのだが）ちょうど $(-L,0)$ に音源があるものとして出てくる波の関数形である

$\phi_r(x,y,t)=F(\sqrt{(x+L)^2+y^2})\sin[2\pi f(t-\frac{\sqrt{(x+L)^2+y^2}}{c})+\psi]$

で与えられる（当然のことながら、音速と周波数は変わらない）。ここで $\psi$ は反射で位相がずれるかもしれないので導入した定数で、「流体が壁を通り抜けて出入りしない」という条件から後で決める。速度の $x$ 成分は速度ポテンシャルの $x$ 方向の偏導関数なので

$u_s(x,y,t)=\frac{\partial\phi_s}{\partial x}=\{F'(\sqrt{(x-L)^2+y^2})\sin[2\pi f(t-\frac{\sqrt{(x-L)^2+y^2}}{c})]\\-[2\pi\lambda F(\sqrt{(x-L)^2+y^2})]\cos[2\pi f(t-\frac{\sqrt{(x-L)^2+y^2}}{c})]\}\frac{x-L}{\sqrt{(x-L)^2+y^2}}$

$u_r(x,y,t)=\frac{\partial\phi_r}{\partial x}=\{F'(\sqrt{(x+L)^2+y^2})\sin[2\pi f(t-\frac{\sqrt{(x+L)^2+y^2}}{c})+\psi]\\-[2\pi\lambda F(\sqrt{(x+L)^2+y^2})]\cos[2\pi f(t-\frac{\sqrt{(x+L)^2+y^2}}{c})+\psi]\}\frac{x+L}{\sqrt{(x+L)^2+y^2}}$

であるから、 $x=0$ での速度の $x$ 成分は

$u_s(0,y,t)=\{F'(\sqrt{L^2+y^2})\sin[2\pi f(t-\frac{\sqrt{L^2+y^2}}{c})]\\-[2\pi\lambda F(\sqrt{L^2+y^2})]\cos[2\pi f(t-\frac{\sqrt{L^2+y^2}}{c})]\}\frac{-L}{\sqrt{L^2+y^2}}\\=-G\sin[2\pi f(t-\frac{r_0}{c})+\alpha]\frac{L}{r_0}$

$u_r(0,y,t)=\frac{\partial\phi_r}{\partial x}=\{F'(\sqrt{L^2+y^2})\sin[2\pi f(t-\frac{\sqrt{L^2+y^2}}{c})+\psi]\\-[2\pi\lambda F(\sqrt{L^2+y^2})]\cos[2\pi f(t-\frac{\sqrt{L^2+y^2}}{c})+\psi]\}\frac{L}{\sqrt{(x+L)^2+y^2}}\\=G\sin[2\pi f(t-\frac{r_0}{c})+\psi+\alpha]\frac{L}{r_0}$

ここで $r_0=\sqrt{L^2+y^2}$ , $G=\sqrt{[F'(r_0)]^2+[2\pi\lambda F(r_0)]^2}$ , $G\cos\alpha=F'(r_0)$ , $G\sin\alpha=-2\pi\lambda F(r_0)$ である。

ここで「流体は壁抜けをしない」すなわち速度の壁に垂直な成分 $u_x$ はゼロになる $u_r(0,y,t)+u_s(0,y,t)=0$ という条件を課すと*2

$Q\sin[2\pi f(t-\frac{r_0}{c})+\psi+\alpha]\frac{L}{r_0}-Q\sin[2\pi f(t-\frac{r_0}{c})+\alpha]\frac{L}{r_0}=0$

よって $\psi=2n\pi$ ( $n$ は整数)となる。これより反射波の速度ポテンシャルの関数形は

$\phi_r(x,y,t)=F(\sqrt{(x+L)^2+y^2})\sin[2\pi f(t-\frac{\sqrt{(x+L)^2+y^2}}{c})]$

となる（どうせグラフを描いたら同じ形になるから $\psi=2n\pi$ は消した）。この「速度ポテンシャルは剛体壁での反射で位相が変わらない」という式は「密度、圧力の場の時間変動部分は剛体壁の反射で位相が変わらない」という式でもある（これや高校物理のジャーゴンでは「自由端反射」という）。

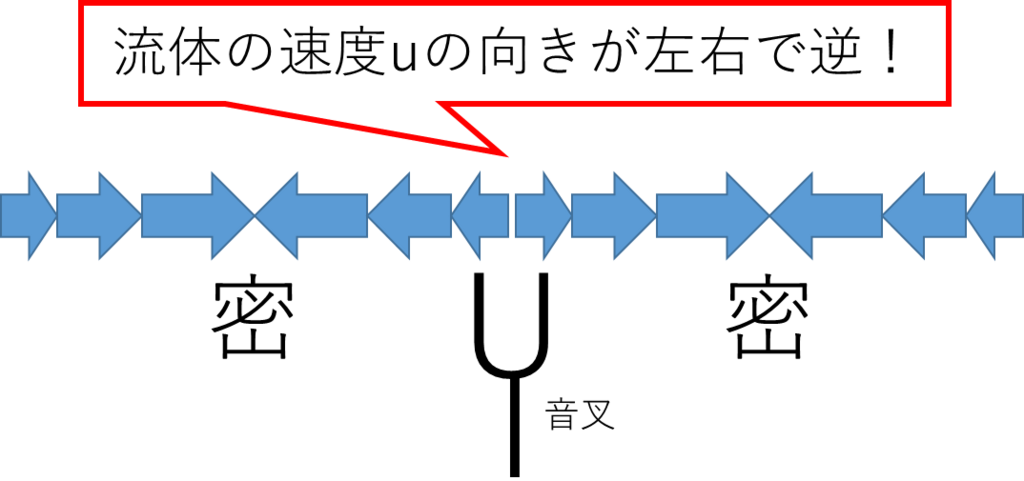
これに対して速度の $x$ 成分は入射波と反射波の符号が壁で逆転する。ここが問題文中の「音波の反射条件は固定端反射とみなす」という表現に相当する。ついでに言うと速度の $y$ 成分は壁では符号は変わらない。

次に波の干渉について考えよう

波の干渉で次の図を見たことがあるだろう：

f:id:arakik10:20180122080522g:plain

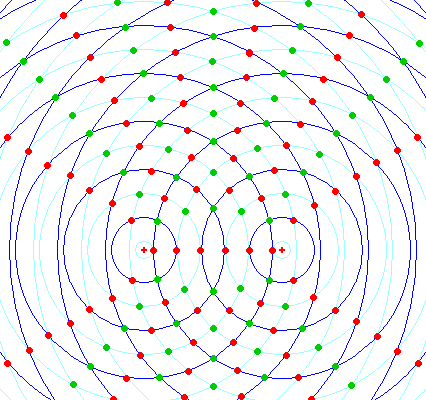
図版出典：波の干渉 ■わかりやすい高校物理の部屋■(2018年1月22日アクセス)

http://wakariyasui.sakura.ne.jp/p/wave/housoku/kannsyou.html

ここで同心円は「何」を表しているのだろうか？音波の問題の場合は「速度ポテンシャル」「圧力（∝密度）」の等高線を表している。京大入試の物理の問題の場合は、壁での反射なので、図は次のようになる（図は上図を改変したもの）：

f:id:arakik10:20180122081139p:plain

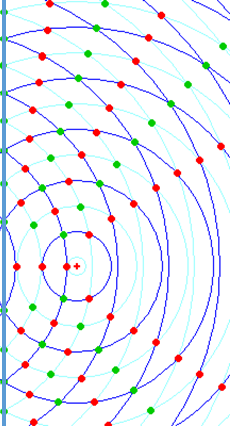
壁があるので、壁での反射波との干渉になる。先の計算の結果を考えると、反射波のポテンシャル（や圧力）は丁度、壁の反対側に同位相の音源があるものと見なした波になっている。つまり「壁が無いと思って2個の音源の干渉を求める」問題と等価になる（図は上図を改変したもの）：

f:id:arakik10:20180122081403p:plain

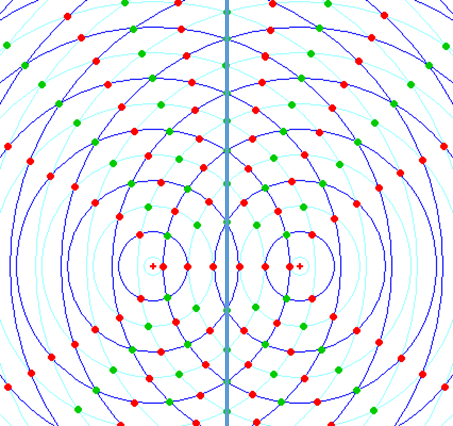
では車をy方向に動かして干渉の様子を見よう

時刻 $t=0$ に位置 $(-L,0)$ にあった音源から出た音を、時刻 $t=T$ に位置 $(L,-UT)$ で聞くと、音の速度ポテンシャルの値は

$\phi_r(L,-UT,T)=F(\sqrt{(2L)^2+(UT)^2})\sin[2\pi f(T-\frac{\sqrt{(2L)^2+(UT)^2}}{c})]$

時刻 $t=T$ に位置 $(L,-UT)$ で車が出すの音の速度ポテンシャルの値は

$\phi_s(L,-UT,T)=F(0)\sin(2\pi fT)$

これより2個の速度ポテンシャルが逆位相となる条件は $2\pi f\frac{\sqrt{(2L)^2+(UT)^2}}{c}=(2 n+1)\pi$ （ $n$ は整数）となる。ここで大事な条件がもう一つあって、距離 $\sqrt{(2L)^2+(UT)^2}$ は音が時間 $T$ をかけて、えっちらおっちらやってきた距離なので $\sqrt{(2L)^2+(UT)^2}=cT$ でもある。だから $T=\frac{2L}{\sqrt{c^2-U^2}}$ の条件がつく。逆位相の条件は $2\pi fT=(2 n+1)\pi$ でもあるから、 $T=\frac{2n+1}{2f}$ である。ゆえに $\frac{2n+1}{2f}=\frac{2L}{\sqrt{c^2-U^2}}$ すなわち $\displaystyle L=(n+\frac{1}{2})\frac{\sqrt{c^2-U^2}}{2f}$ となる。ちゃんと解ける。出題ミスはない（阪大みたいな採点ミスはあるかどうか分からない）。

f:id:arakik10:20180123090501p:plain

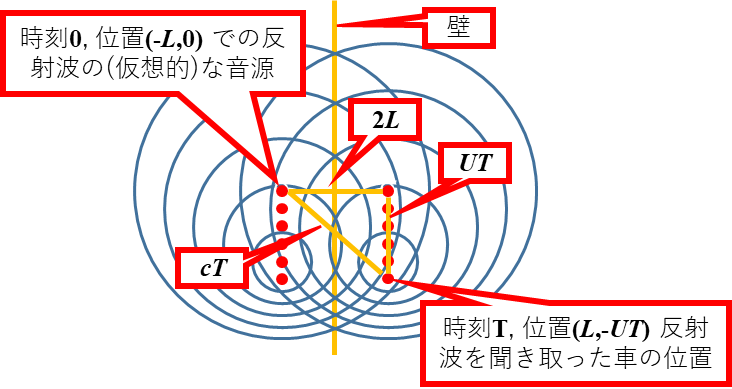
注：この図版は1月23日に作製し、追加

固定端反射？

以上の計算では現象を記述する物理量として速度（とそのポテンシャル）と圧力と密度を用いた。音波は一つの物理量では記述できない自然現象である（ただし一つの物理量の方程式に落とし込んで解を求めるのは常套手段のひとつである）。速度の壁方向の成分は固定端反射（高校物理語）だが、圧力や速度ポテンシャルは自由端反射（高校物理語）である。しかも波が境界に対して斜めにぶつかっている。位相の条件を求めるには「（速度あるいは「変位」が）固定端反射」という表現は「ウソではないが正答を導くには厳しすぎる」気がする。

[1.23追記]しかし、逆に出題者の立場に立って考えてみよう。解答者は指導要領に縛られないが、出題者は指導要領に縛られる。指導要領の範囲内で音波の反射の条件を表現しようとすると、典型的な例題としては「気柱の共鳴」が考えられるが、これと類似の状況を記載するとすれば「音波の反射条件は固定端反射とみなす」以外の書きようがないのではないか。ここにいちゃもんをつけているとすれば「揚げ足取り」も甚だしい。[1.23追記終わり]

[1.24追記]では受験生の側では、この問題にどのような対策があるだろうか。（高校教師、予備校教師とは言っていない。彼ら彼女らは大学で科学の学び方を学んでいるはずである。大学以上の知識を動員して理解を進め、高校生のための知識に落とし込む努力をすべきである。）まず「点音源」だが、左右対称(1次元)軸対称(2次元)(球対称(3次元))なモードが出ていると前提して計算をする場合には

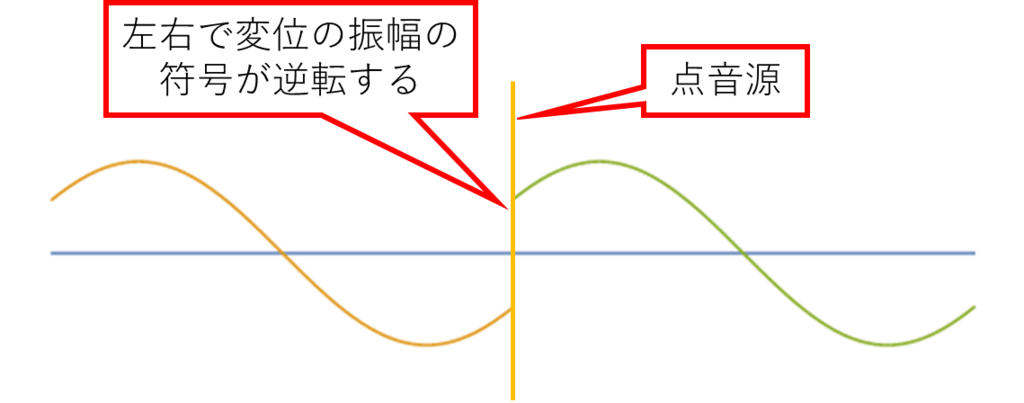
「変位」で考えた場合、音源の位置で振幅が逆になる

ことを理解しておくべきである*3：

f:id:arakik10:20180115060712p:plain

f:id:arakik10:20180124080052p:plain

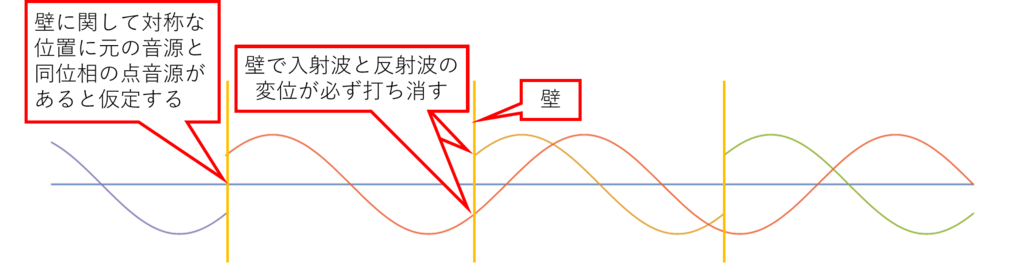
次に、壁による「音波の固定端反射」のときには、

壁に対して音源と対称な位置に同位相で振動する仮想的な音源がある

として、波の位相を計算するとよい。なぜなら壁の位置で「元の音源から左に走る波の変位」と「仮想音源から右に走る波の変位」が必ずちょうど壁の位置で振幅が常に逆になり、重ねると変位がゼロになるからである：

f:id:arakik10:20180124080258p:plain

この二つの物理的に高校の物理の範囲で教えることのできそうな知識を備えていれば、京大の問題は壁の向こうに仮想的点音源からの波の問題として取り扱うことができる。[1.24追記終わり]

点音源と波の速度の向き

波の干渉を教えるときに、点状の振動源を2個ならべて、直進する波の行路差から位相がかみ合う場所を求めるのはお約束のメソッドである。このときに波の進む向きを気にしたことがあるだろうか？

f:id:arakik10:20180122112710p:plain

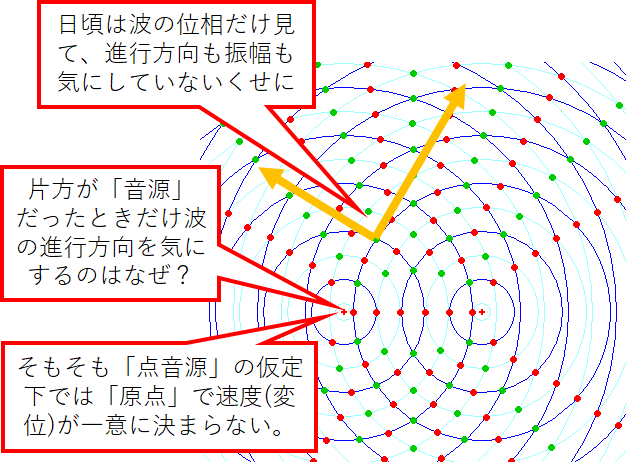
位相が揃うかπずれるかしか見ていない。そもそも音波の干渉で「変位」という向きを持った量（ベクトル場）で議論するのは筋が悪すぎで、スカラー量である圧力、密度、速度ポテンシャルを使う方が良い。でもこれを高校物理に落とし込むのは結構、きついかなあ。まあそんなことゆうと「固定端反射」も「天下り式」だしいｗｗｗｗｗ

よしだひろゆき氏のPDFに「なお、直接波と反射波が運転手の位置で斜めに交差する場合は、高校物理の範囲では議論できない」と書いてあったのを見て、ボクは目が点になってしまった。この人、波の干渉で何を教えてるんだ？

*1:計算に用いる技法はなるべく高校数学に近い部分で済ませたいので、 $\sin$ を使い、初期位相を固定した。