例の入試ミス関連で、いくつかのブログやツイッターやPDFを見たけれど、高校数学の範囲内の数式を使って計算をきっちりと書いたものに出会えなかったので書いた。くだんのSEGの先生のメール*1やPDF*2を見たが、いかにも「受験物理のお行儀の良い答案」みたいな記述で、これでは天下の阪大の大先生たちを説得できはしないだろうと思う。たぶん「12月により詳細な指摘」(朝日新聞,1月6日)で数式を使った議論が出て、ようやくねじ伏せられたのだろう。理系の研究者は日頃から「論文の査読」というシステムでバトルしているので、そうそう簡単に説き伏せることはできないものである。
鉄1kgと綿1kg重いのは…
阪大の出題ミスで「阪大の言い訳」を朝日新聞で読んだとき、こんなクイズを思い出した「鉄1kgと綿1kg、重いのはどっち?」。こいつに「どちらも同じ」と答えたときに、「大気から受ける浮力の分だけ綿の方が軽い(kgって質量の単位だよね)」と返されたような気分になった。*3どこまでを「前提」としてるんだ?朝日新聞の図を引用しよう。
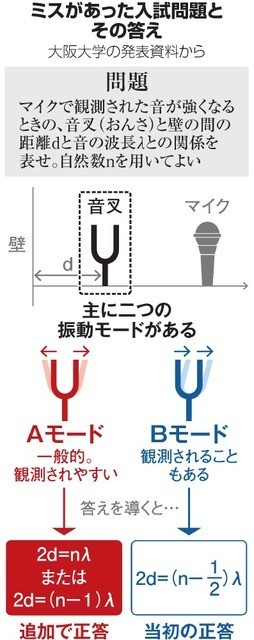
この「音叉の問題」の全体を見ると、しょっぱなの問題がこれである

きっちりとAモードの振動で疎密波の方向分布を問うている。ここから始めておいて、最後の問題だけ「Bモードもあるよ」ってのはちゃぶ台返しである。*4

Google検索の結果(2018年1月15日アクセス)
愚痴、あるいはなぜ阪大ははまったのか?
出題者の学部学科なんて絶対に表に出ない。でも、これだけは言えるが、実は日本の大学の「理学部・物理学科」で流体力学を研究してる先生はほとんどいないのだ。いまの「物理学科」は量子力学が大好きで、流体力学を本格的に学びたいならば「宇宙物理学」「地球物理学」「機械工学」「航空工学」「核融合」といった学科、分野に進む方がいい(それとも東大理、京大理をめざす?)。今回も流体力学に慣れていないのでドツボにはまったのでは、と邪推している(てゆーか、受験物理で音波の反射は鬼門だという意見もツイッターとかで見た)。
波ってどのように式で表すのだろう?
まずは次のグラフを見て、これが「右に進む波」なのか「左に進む波」なのか分かるだろうか?

正解は「わからない」である。波の山や谷が次の瞬間にどちらに動くかという情報が無いので何とも言えない。ではどちらに動くかということを数式ではどのように表すのだろう?答えは音源の位置をとして次のようになる:
右(>0の方向)に進む波:
左(<0の方向)に進む波:
ここでは音源の周波数、
は音速。この式の意味は、波の山が
の位置にあったとすると、音源がその山を作ったのは
秒前だということ。波を表す関数は時刻と位置の関数だから「2変数関数」という高校数学の範囲外の関数が現れる。でも、どちらも三角関数の引数の中にお行儀良くあらわれているので、慣れれば大したことないと思う。
波の伝搬と反射の設定と計算
まず音叉から出る右(正方向)と左(負方向)に進む音波をA-1(問1)の状況をきっちりと考慮に入れ、
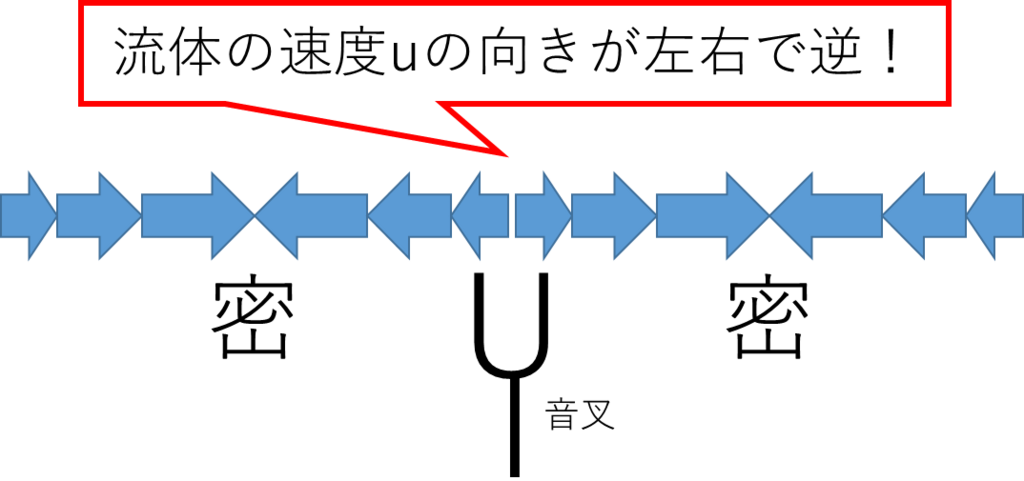
密度の分布が音叉に対して左右対称になるように、速度を次式で与える(振幅を1と置き、減衰はしないとした)*5:
(ただし
>0),
(ただし
<0),
ここでは音源の周波数、
は音速。ここで音が反射する壁での状況を考える。壁(
)での「壁への入射波」
は
となる。ここで「壁からの反射波(右に進む波)」を
と置く(音速、周波数は反射で変わらないことを使った)。反射波の振動は山と谷がどこに来るかわからないので、位相にを入れておく。ここで未知数
は、壁(
)での条件である「空気は壁を突き抜けて進むことはない」ことより
が常に成り立つこととなるから*6、
ここでは整数。これより反射波を表す関数は
となる。この反射波が音叉から右方向に出る音波と共鳴する条件は次のようになる:
(ただし
>0),
ここでは整数。 ここで波長
が
で与えられることを考慮すると、求める条件は
(ここで
は整数)
となる。
SEGの参考書は書店で拝見したことがあるが、SEGで学ぶ国公立理系上位校ねらいの生徒たちなら、これくらいの数式くらい簡単にフォローできるだろう。
入試出題採点経験者として言うが、出題者は学習指導要領に縛られるが、解答者は縛られる必要は全くないのである。
*1:https://www.dropbox.com/s/2vlzte1toqrgsf2/大阪大.pdf?dl=0
*2:https://www.dropbox.com/s/z5x1pq7k7i8daoy/osaka_u.pdf?dl=0
*3:こうゆうのをネットスラングで「小並感」というwwwww
*4:気づくのが遅すぎて、採点のやり直しもへったくれもない状況だったので、強弁せざるをえなかったんだろう。また、問5の設定から、問4の解答を逆算することもできるので、入試問題としてはいまいちかもしれない。
*5:出題者は左右の速度の設定でこけたのか?
それともう一つ。ここでの音叉から出る音は4重極放射なので、波の振幅が変わらないとした仮定はかなり非現実的かもしれない。
*6:これは学習指導要領の高校物理の範囲内では「固定端反射」に相当する。ちなみにここで壁は音が当たっても振動しないことになっているので、壁の向こう側に音は伝わらない。だからこの実験をレオパレスでやることはお勧めできない…ような気がする。